论文笔记--Weakly-Supervised Multi-Face 3D Reconstruction
摘要
三维人脸重建在媒体应用领域扮演着重要的角色,其中包括数字娱乐,社交媒体,情感分析和人物辨识。利用单张图片估计人脸参数模型,首先需要检测面部区域和面部关键点坐标,然后裁剪出每个人脸区域,利用深度学习方法对该区域图片进行参数回归预测。
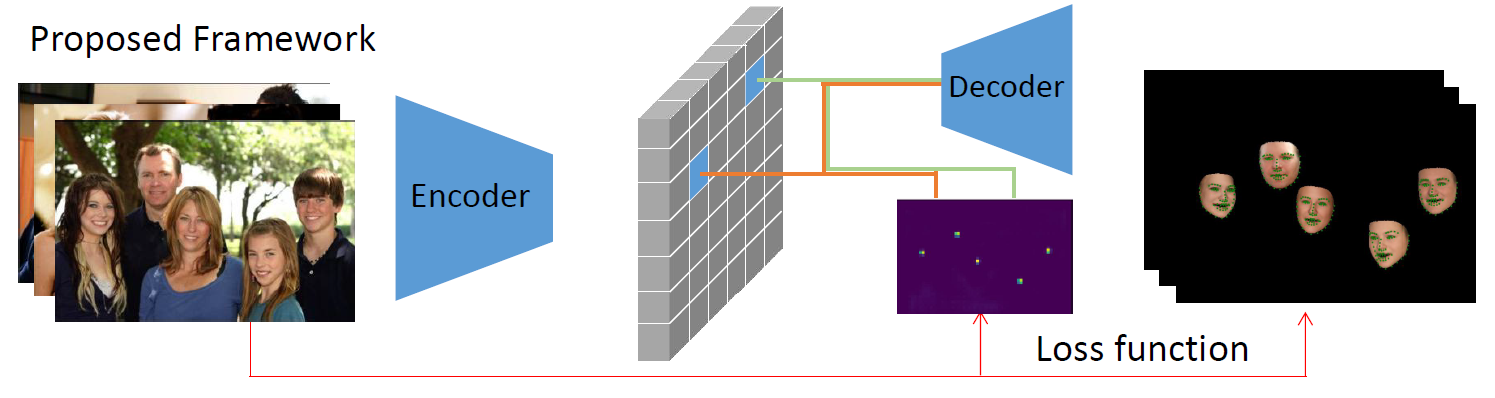
不同于常规方法(对每个检测人脸区域独立的预测),本文提出一种端到端的多个面部三维重建方法(Multi-Face Reconstruction),可以利用单个网络推理预测出多个人脸实例参数。与此同时,本文为每个图像中的人脸使用了全局相机模型,使得重建出来的头部位置和面部朝向都与原图相同。
本文提出的方法不仅可以减少特征提取过程中的计算冗余,而且网络模型也更加容易部署。
基本介绍
常规的方法都是将人脸校正到特定的帧图片上,首先利用检测器定位面部区域和面部坐标,然后对面部进行裁剪后输入到神经网络,整个的过程包含了面部检测和面部参数回归估计两项任务。
局限性
相比于前几年单目图片重建方法,很少有工作专注于单目重建多个面部。其次,进行多面部重建的方法,只重建了面部形状,而忽视了面部纹理,光照信息;而且这些方法大多是以监督学习的方式进行训练,需要大量的几何细节ground-truth。由于训练样本要么是通过渲染合成的,要么是从传统的基于优化的方法中获得的,因此它们通常对姿势和光照的变化不太鲁棒。
本文提出的方法是一张图片里多个人脸共享相同的相机参数,这意味着相机焦距和相机中心坐标在3D参数模型上是一致的。而常规的方法是一个人脸对应一个相机模型参数,忽视了在3D视角下每个个体的头部位置和朝向这些高阶语义信息。
创新点
- 提出一个弱监督多面部重建网络框架,仅用一次前向传播就可以预测多个人脸实例的拟合3DMM模型参数
- 提出能够在3D场景中恢复相对头部位置和面部朝向的全局相机模型
- 阶段式训练方法,优化整体网络架构
方法
计算耗时比较

\[ 常规方法耗时:T_c = T_{Encoder} + n·(T_{Rectify}+T_{Encoder'}+T_{Decoder}) \]\[ 本文方法耗时:T_p = T_{Encoder} + n·T_{Decoder} \]
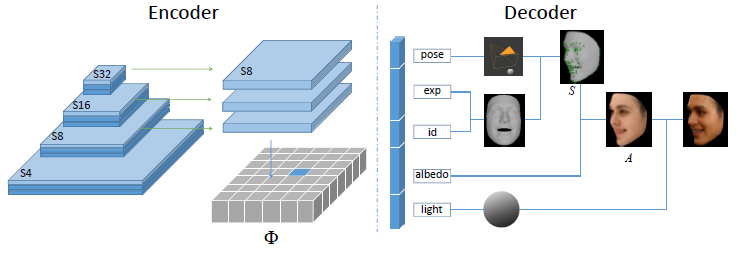
网络结构
\[\delta=(\delta_m,\delta_{id},\delta_{exp},\delta_{alb},\delta_{pose},\delta_{illum}) \]\[ \delta_{m}\in{\mathbb{R}^{1}}, \delta_{id}\in{\mathbb{R}^{80}}, \delta_{exp}\in{\mathbb{R}^{64}}, \delta_{alb}\in{\mathbb{R}^{80}}, \delta_{illum}\in{\mathbb{R}^{27}}\]
Encoder输出258个参数\(\delta\),包含有身份\(\delta_{id}\),表情\(\delta_{exp}\),反照率\(\delta_{alb}\),姿态\(\delta_{pose}\),光照\(\delta_{illum}\),图片每个人脸位置\(\delta_m\)
3DMM
3DMM作为Decoder,参数化方法合成人脸,人脸的形状,纹理表示如下:
备注:3表示x, y, z三个坐标值;N表示顶点数
\[ S = \bar{S} + \delta_{id}*S_{id}+\delta_{exp}*S_{exp} \]\[ A = \bar{A} + \delta_{alb}*A_{alb} \]\[ S\in{\mathbb{R}^{3 \times N}}, A\in{\mathbb{R}^{3 \times N},N=35709} \]
相机模型
透视投影矩阵: \(f_g是焦距,w和h是图像的宽和高\) \[ K = \begin{bmatrix} f_g & 0 & w/2 \\ 0 & f_g & h/2 \\ 0 & 0 & 1 \end{bmatrix} \]
旋转矩阵:\(R\in{\mathbb{R}^{3 \times 3}}\),由\(\delta_{rot}\in{SO(3)}\)计算得到。\(\delta_{rot}\)包含三个参数,分别是沿着x轴,y轴,z轴旋转角度
平移矩阵:\(t=\begin{bmatrix}t_x & t_y & t_z\end{bmatrix}^T\);平移矩阵内部参数的计算取决于预测的平移向量\(\delta_{trans}=\begin{bmatrix}d_x & d_y & d_z\end{bmatrix}^T\)决定。(备注:\(c_x,c_y\)是每个人脸在图像平面的中心位置) \[ \begin{bmatrix} t_x \\ t_y \\ t_z \end{bmatrix} =\begin{bmatrix} d_z(d_x+c_x-w/2)/f_g \\ d_z(d_y+c_y-h/2)/f_g \\ d_z \end{bmatrix} \]
姿态系数:前文提到的姿态系数\(\delta_{pose}=(\delta_{rot},\delta_{trans})\)
图像空间坐标表示:\(p\propto{K(RX+t)}, p=(u,v,1)^T\)
损失函数
整体损失函数有5项函数构成,分别叫center loss,pixel-wise loss,perception-level loss,sparse landmark reprojection loss,regularization loss。其中后面三项的函数设计的思路或者内容与CVPR Workshop2019论文的损失函数一致
后续补充损失函数介绍~~~